Algoritmos No Lineales
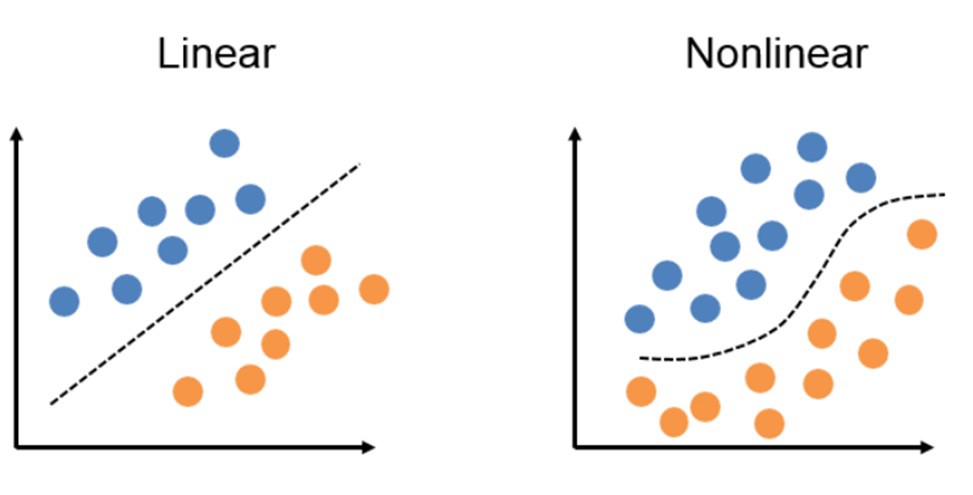
La diferencia fundamental entre los algoritmos lineales y los no lineales es que estos últimos son capaces de utilizar funciones de cualquier grado de complejidad, lo que permite crear funciones de predicción mucho más complejas que los métodos lineales. Este aumento de complejidad, si bien requiere mucho mayor cantidad de procesamiento, también permite un analisis mucho más profundo de los datos para ajustar el modelo lo más cerca posible de la realidad, lo que en consecuencia, implica la habilidad de crear modelos capaces de analizar imágenes, videos, patrones muy complejos, entre otros (Básicamente, problemas donde la entrada no está linearmente relacionada con la salida).
Support Vector Machines
SVM o Support Vector Machine es un algoritmo creado para la clasificación de datos y problemas de regresión. Puede resolver tanto problemas lineales como no lineales y consiste en la creación de lineas o hiperplanos para separar los datos en dos clases.
En problemas linearlmente separables , el algoritmo hace un procedimiento similar a la Regressión lineal en el sentido de que busca encontrar una recta que separe los datos de tal manera que la distancia entre todos los puntos a la linea sea mínima. Esto se hace buscando el punto de cada una de las clases que se encuentre lo más cerca a la recta posible, los cuales se llaman Support Vectors. Luego de computada la distancia entre los support vectors y la línea es que conseguimos un margen. El objetivo es maximizar el margen para llegar a la recta óptima.
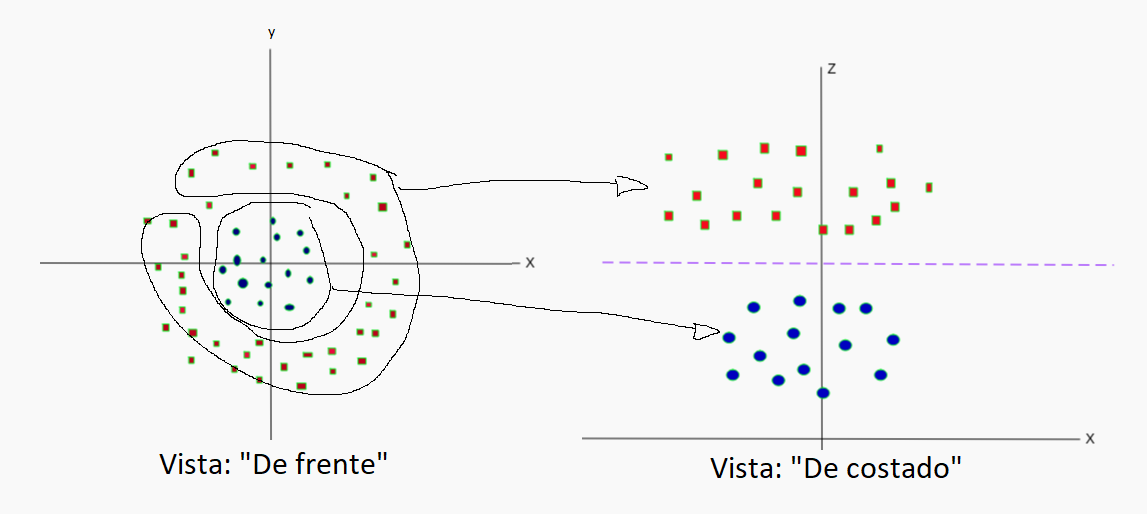
En problemas no linearmente seprables, por ejemplo, en forma de anillo, se le agrega una dimensión extra a los datos lo cual nos permite ver "de costado" estos datos y crear lo que será una linea que los separe, aunque luego esta linea vista nuevamente "de frente" se terminará representando como un anillo. Esta nueva dimensión se representa con un vector nuevo Z tal que Z = X^2 + Y^2
Decision Trees
Decision trees o árboles de decisión es un algoritmo, que al igual que SVM, sirve para la resolución de problemas de regresión y clasificación. Consiste en la formación de un árbol reverso donde se comienza de una raiz y a partir de ella se crean ramas que, según condiciones aprendidas de los datos de entrenamiento, se decide si bajar por una rama o por otra. Cada nodo del arbol se separa en más ramas hasta culminar en hojas, las cuales determinan la salida del modelo.
Supongamos un ejemplo muy básico:
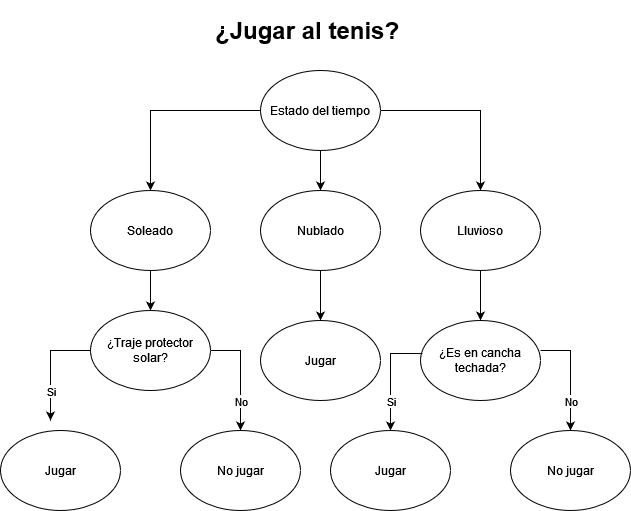
En este ejemplo, ya tenemos modelada una situación común de la vida y en base al nodo que tomemos, la decisión de jugar o no al tenis. Por ejemplo, si el día es nublado, jugaremos siempre. Si el día es lluvioso, jugaremos solo cuando la cancha sea techada. Por último, si el día es soleado, jugaremos solo si tenemos protector solar puesto.
Los nodos y decisiones de este algoritmo pueden ser creadas con varias fórmulas. Entre ellas, tenemos el índice de Gini, el cual indica que tan bien estan mezclados los datos en un atributo. El atributo con mayor índice de gini es aquel seleccionado como la condición del primer nodo y luego para el resto de los nodos, se utilizaran el resto de los atributos dependiendo de la partición realizada en el paso anterior y al indice de gini máximo siguiente al nodo raiz.
Conclusiones
Se presentan dos de los algoritmos más básicos para la resolución de problemas no lineales. En el repositorio de este portfolio, se encuentran pequeños trabajos realizados academicamente con problemas concretos para una mejor visualización de estos algoritmos además de otros como K-nn y Naive Bayes.